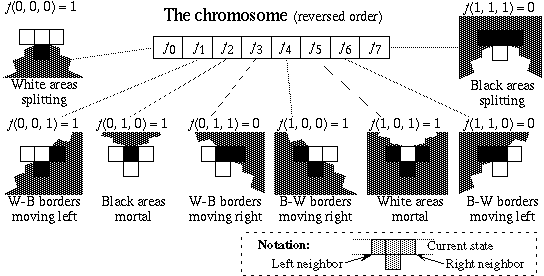
4. Interpretation of the Chromosome and Patterns

Some characteristics of the patterns, shown in the previous section, generated by 1D-ACA can be explained by the chromosomes of the automata. This explanation is applicable to both randomized and interlaced automata, but not applicable to synchronous automata, nor to partially synchronized models called ``independent clocks'' [Ing 84].

The chromosome, or the look-up table, contains eight genes, f0, f1, ..., f7, each of which is one-bit length. These genes can be interpreted as follows.

f0: If its value is 1, white domains may split into two. Otherwise, they do not split.
f7: If its value is 0, black domains may split into two. Otherwise, they do not split.
f2: If its value is 0, black domains are mortal (may die). Otherwise, they are immortal.
f5: If its value is 1, white domains are mortal. Otherwise, they are immortal.
f1: If its value is 1, WB borders (white-to-black borders) may move left. Otherwise, they do not move left.
f6: If its value is 0, BW borders (black-to-white borders) may move right. Otherwise, they do not move right.
f3: If its value is 0, WB borders may move right. Otherwise, they do not move right.
f4: If its value is 1, BW borders may move left. Otherwise, they do not move left.

Detailed explanations on the gene functions are omitted because of page limitations. However, the functions can be understood intuitively by Figure 16. This figure shows the current state of a cell to be updated, those of the neighbor cells, and the updated state of the cell. For example, the leftmost part of the figure shows the case that all three cells are white (0's). The next state is specified by gene f0 . If the updated state is black as shown in the figure, this is the beginning of a black domain, and the white domain splits into two. Other parts of the figure can be interpreted in the same way.

Figure 16. Interpretation of the chromosome

Several examples shown in the previous section are analyzed using the interpretation above.

#226 (= 11100010): Firstly, gene f0 is 0 and gene f7 is 1. Thus, both white and black domains in patterns C1 and C2 do not split. Secondly, f2 is 0 and f5 is 1. Thus, both white and black domains are mortal. Black domains actually die in C1 and C2. All the black domains die if the random order is used. However, some black domains continue to exist if the interlaced order is used, because gene f7 is not used for the state transitions of such domains. Thus, the properties of the automata are only partially expressed when no noise exists. Thirdly, f1 is 1 and f3 is 0. Thus, WB borders can move in both directions. They actually move in both directions in C1. However, they move in single direction in a period in C2. This is another example of partial expression of genes under noise-free situations. Fourth, f6 is 1 and f4 is 0. Thus, BW borders do not move. This property is expressed both in C1 and C2.

#166 (= 10100110): f0 is 0 and f7 is 1. Thus, both white and black domains in patterns F1 and F2 do not split. Both f2 and f5 are 1. Thus, black domains are immortal and white domains are mortal. White domains die in C1, but they continue to exist after the automaton comes into a limit cycle in C2. This is another example of partial expression of genes. Expression and suppression of other genes can easily be observed.

#58 (= 00111010): Black domains can split because f0 is 0, but white domains do not split because f7 is 0. Expression of gene f0 can easily be seen in G1, but this property is also suppressed in G2. Expression and suppression of other genes can easily be observed.

Other patterns, such as those shown in Sections 3.1 to 3.3, can be explained in the same way.

The above simpler relation between the look-up table values and the property of patterns exist only if the computation is asynchronous (sequential). Synchronous or partially synchronous (partially concurrent) automata cannot be mostly explained using the above interpretation. It is much more difficult to analyze these automata. The existence of the above relation seems to relate to some conservation law, which is broken in synchronous or partially synchronous automata.

Go to: Next section, Parent node

Y. Kanada