数日まえから 3D プリンタでセル・オートマトン風のパターンを印刷しているが,これはちょっとおもしろいから,よのなかにだしたい. とりあえずは「自然な方向の印刷」だけ出品しようとしていた Maker Faiere にこれもだそうとおもう. さらに学会にもだすことをかんがえているが,それにあたっては数理モデルがあったほうがよい. というわけで,数理モデルというか計算モデルの構築をめざしてみた.
セル・オートマトンの印刷をするときは,プリントヘッドに円をえがかせて,すくなくとも 1 回転するあいだは (方向はかえるが) 定速で移動させる. また,フィラメントのおしだし速度も一定だ. これをシミュレートするモデルを構築してみた.
セル・オートマトンは 1 列ぶんいっぺんに,つまり同期して計算するのが普通だが,「3D プリンタがつくりだす,セル・オートマトン風のパターン」 に書いた 「ランダムな非同期セル・オートマトン」 と同様にこの 3D 印刷でも非同期的に印刷する (というより,同期して印刷するのは 1 列を並列に印刷するということだから,3D プリンタで実現するのは困難だ. そのためだろう,生成されるパターンも類似している.
つくったモデルでパターンを生成して,それを 3D プリンタにかけるときと同様に G-Code に変換して Repetier MAC で視覚化した例をいくつかあげる. これを 3D プリンタにかけても (よほどゆっくり印刷すればべつかもしれないが) このかたちにはならないのだが,視覚化するにはよい方法だ.

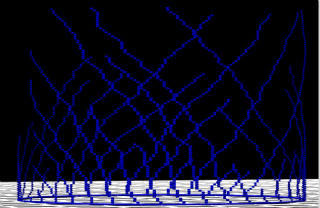
これらはいろいろパラメタをかえて,実際の印刷物 (下の写真) ににせたものだ. パターンが成長する角度などは実際のものにちかづけている. それでも,実際の印刷物ではパターンが分岐したり融合したりしているところがシミュレートできていない. そこまでシミュレートできる方法がわかるとよいが,そうでなくても論文のネタにはなるだろう.



