Kanada, Y., Artificial Life IV, Poster, 1994.
[ English page ]
[ 論文 PDF ファイル ] [ ポスター ハイパーテキスト版 ]
[ 未出版 拡大版論文 PDF ファイル]
要旨 (英語のみ):
Cellular automata are used as models of emergent computation and
artificial life. They are usually simulated under synchronous and
deterministic conditions. Thus, they are evolved without existence
of noise, i.e., fluctuation or randomness. However, noise is
unavoidable in real world. The objective of the present paper is to
show the following two effects and several other effects caused by
asynchronism or synchronism and by existence or nonexistence of
randomness in the computation order in one-dimensional asynchronous
cellular automata (1D-ACA) experimentally. One major effect is that
certain properties of two-neighbor 1D-ACA are fully expressed in their
patterns if certain level of randomness exists, though they are only
partially expressed if no randomness exists. The patterns generated
by 1D-ACA may have characteristics, such as mortality of domains of 1's
or splitting domains of 0Us into two. These characteristics, which are
coded in the RchromosomeS of the automata, i.e., the look-up table, are
fully expressed only when the computation order is random. The other
major effect is that phantom phenomena, which almost never occurs in
real world, sometimes occur when there is no noise. The
characteristics of patterns generated by several 1D-ACA are drastically
changed from uniform patterns to patterns with multiple or chaotic
phases when only low level of noise is added.
参考文献:
"非同期セル・オートマトン". Wiki Pedia,
この論文のオリジナルな点がかんたんに説明されています.
研究テーマ紹介:
RACA: ランダムな非同期セル・オートマトン
キーワード: ランダム・セルオートマタ, ランダム・セルオートマトン, ランダム・セル・オートマタ, ランダム・セル・オートマトン, ランダム化セルオートマタ, ランダム化セルオートマトン, ランダム化セル・オートマタ, ランダム化セル・オートマトン, 非同期セルオートマタ, 非同期セルオートマトン, 非同期セル・オートマタ, 非同期セル・オートマトン, 創発的計算, 複雑系, ノイズ, エマージェント・コンピュテーション, セルラオートマタ, セルラオートマトン, セルラーオートマタ, セルラーオートマトン, セルラ・オートマタ, セルラ・オートマトン, セルラー・オートマタ, セルラー・オートマトン, ランダマイズド計算, 規則ベース計算
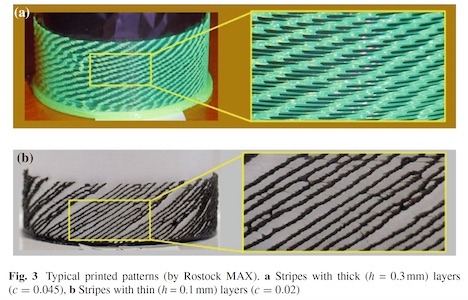
 要旨: 3D printing technology usually aims reproducing objects deterministically designed by 3D CAD tools. However, 3D printing can generate patterns similar to randomized (non-deterministic) 1D or 2D cellular automata (CA). Cheap fused deposition modeling (FDM) 3D printers can be used for this purpose. By using an FDM 3D printer, melted plastic filament is extruded by a hot nozzle to shape a 3D object. They can generate CA-like patterns with constant head motion and constant filament extrusion and with unintended fluctuation but no explicit randomness. Because of fluctuation, every time the printer generates a different emergent pattern. This paper proposes a method for printing seaweed-like patterns of 1D and 2D CA using FDM, and computational CA models. This method will open a new horizon of 3D printing applications.
要旨: 3D printing technology usually aims reproducing objects deterministically designed by 3D CAD tools. However, 3D printing can generate patterns similar to randomized (non-deterministic) 1D or 2D cellular automata (CA). Cheap fused deposition modeling (FDM) 3D printers can be used for this purpose. By using an FDM 3D printer, melted plastic filament is extruded by a hot nozzle to shape a 3D object. They can generate CA-like patterns with constant head motion and constant filament extrusion and with unintended fluctuation but no explicit randomness. Because of fluctuation, every time the printer generates a different emergent pattern. This paper proposes a method for printing seaweed-like patterns of 1D and 2D CA using FDM, and computational CA models. This method will open a new horizon of 3D printing applications.